6.2 Permutaciones.

En varios de los ejemplo anteriores usamos el principio de la multiplicación en una situación muy especial: en cada posición, siempre teníamos las mismas opciones (como en el ejercicio de la sección anterior que se pedía formas números que solo tenían cuatros y doses). Si hay que llenar n posiciones y cada posición tiene k opciones, el total de arreglos es:

Es importante notar que la formula anterior es valida únicamente cuando en todas las posiciones siempre tenemos la misma cantidad de opciones.

Ejemplo. Se escriben las letras a, b, c, d, e , f en papelitos distintos y luego se resuelven los seis papelitos en una bolsa. Se desea formar palabras de cuatro letras con esas letras. Se extrae un papelito, se apunta la letra, y se regresa a la bolsa, repitiendo este proceso 4 veces ¿cuántas palabras de puede formar?
Las palabras son arreglos de cuatro letras, cada letra puede ser de seis tipos distintos, Entonces el total de palabras es 6⁴ = 1296 palabras.

Otra situación especial que aparece con frecuencia, es que cada vez que hacemos una elección, no podemos volver a escoger esa opción (como en el ejercicio que había que formar números cuyos dígitos no se repitieran). Imaginemos primero que se tienen n objetos y nos preguntamos de cuantas maneras podemos ordenarlos en fila. Como ejemplo concreto, consideremos las 5 vocales, a,e,i,o,u y nos preguntamos de cuantas maneras podemos ordenarlas . Posibles arreglos serian aeiou, ueoia, aioue. Son 5 posiciones y 5 objetos . La primera posición tiene 5 opciones, la segunda 4 (porque ya no podemos usar la misma letra), la tercera 3, la cuarta 2 y la ultima 1. Entonces en total hay 5×4×3×2×1= 120 arreglos.

Hacemos notar que lo importante aquí es que no podemos repetir lo que escogemos. Podemos ver que si en vez de 5 tuviésemos n objetos que ordenar, el total habría sido n (n-1)(n-2)...3×2×1.
Si n es un numero entero positivo, al numero n (n-1)(n-2)...3×2×1 se conoce como n factorial y se representa como n! . Notemos que la definición anterior dice que n! Es un entero positivo una de las propiedades que cumple el factorial es que

Esa propiedad nos dice una manera de “extender” la definición para incluir al cero, ya que entonces 0! seria
Regresando a nuestro problema, podemos enunciarlo con esta nueva notación como sigue:

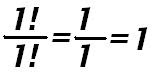
Hay n! Maneras de ordenar n objetos cualquiera.

Ejemplo. Si se tienen 7 libros, el numero de formas de ordenarlos en un librero (uno junto a otro) es 7! = 7×6×5×4×3×2×1= 5040.

Ejemplo si se baraja un paquete completo de 52 cartas.¿De cuantas formas pueden quedar ordenadas?
El número d e arreglos de las 52 cartas es 52!=
80658175170943878571660636856403766975289505440883277824000000000000.