
7.1 Identidades básicas.
Al usar las combinaciones en el capitulo anterior, habían unos casos especiales (cuando los subconjuntos son de un elemento, cuando se escoge todo el subconjunto), que tal vez notaste. A continuación los enunciamos para poder usarlos libremente
Para demostrar la segunda, notamos que cada vez que escogemos k elementos para formar el subconjunto, estamos determinando a los n-k que no estén en el subconjunto. Y viceversa, escoger n-k que no estén en el subconjunto automáticamente determina a los k que si están. Si para cada una elección de unos hay una elección correspondiente de los otros, el total en ambos casos es el mismo ( igual número de formas de escoger los k que sí van a estar y los n-k que no van a estar). Esto es,
La demostración dada es un ejemplo de como se evita la aplicación mecánica de la fórmula, usando un argumento basado en le definición. El siguiente resultado ya no es tan simple y a la vez es muy interesante, se conoce como la identidad de pascal.

Total de subconjuntos con k elementos =
(subconjuntos con k elementos que contienen a a1)
+ (subconjuntos con k elementos que no contienen a a1).
El total es, por definición C (n,.k).Ahora queremos contar cuantos de ellos contienen a a1.
Si uno de tales conjuntos tiene a a1, hay que llenar k-1 posiciones con cualquiera de los otros n-1. En otras palabra, como ya sabemos que a1 es un elemento, hay que escoger k-1 de los n-1 restantes, lo que se puede hacer de C (n-1,k-1) formas.
Para formar un conjunto que no contiene a a1, hay que escoger k elementos de los n-1 que son distintos a a. Esto lo podemos hacer de C (n-1,k)formas. Entonces, por las observaciones de arriba, concluimos que C (n,k)= C (n-1,k-1) + C (n-1,k)
Sabemos contar cuantos subconjuntos de tamaño k tiene un conjunto de n elementos, ¿pero cuántos subconjuntos tiene en total? Hay un conjunto con 0 elementos (el vacío), hay n con un solo elemento, hay C (n,2), que tienen dos elementos,etc. En otras palabras , queremos calcular la suma
Ejemplo: Si el conjunto escogido fuera {q,s,t , escribiríamos 01011 porque solo el segundo, el cuarto y el quinto elementos están en el subconjunto. Si el subconjunto fuera { p,q} la sucesión seria 11000, y al subconjunto vacío le toca 00000. También es claro que si escogemos cualquier sucesión de longitud cinco hecha de unos y ceros, representa algún subconjunto. Por ejemplo la sucesión 10101 es el subconjunto {p,r,t} y la sucesión 00001 es el subconjunto { t}.
Así cada sucesión es un subconjunto y cada subconjunto una sucesión. Entonces contar subconjuntos es lo mismo que contar sucesiones. El principio de la multiplicación nos dice que hay 25 de tales sucesiones. Por tanto, hay 32 subconjuntos.
No había nada especial en que el subconjunto tuviera 5 elementos. Si tuviese n elementos, usaríamos sucesiones de longitud n. El argumento es completamente análogo. De nueva cuenta resumimos nuestro análisis en un teorema.
Teorema 7.3
Un subconjunto con n elementos tiene 2 Un subconjunto con n elementos tiene 2n subconjuntos diferentes.

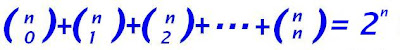
No hay comentarios:
Publicar un comentario