Para terminar esta sección, consideramos el siguiente tipo de problemas: “Dada una colección de
n objetos. ¿De cuantas maneras se peden escoger
k de ellos?
Veamos un ejemplo concreto. El conjunto a considerar será A = {a,e,i,o,u} y nos preguntamos de cuantas maneras se pueden escoger tres vocales. Un primer intento diría:
Como hay que formar arreglos de tres letras a partir de un conjunto que tiene 5 elementos, hay P (5,3) = 60 arreglos.Sin embargo, el razonamiento anterior es incorrecto. Para ver el porqué, imaginemos que las letras escogidas, son, a, i, u. Estas forman los arreglos aiu,aui, iua,iau,uia,uai. Entonces seis diferentes arreglos representan la misma elección . El problema es que aquí no se nos pide el número de arreglos, sino simplemente el numero de formas de escoger las letras. Es decir,
no importa el orden.
Nuestro problema es, que si contamos arreglos, estamos contando seis veces el número que queremos. Esto es así porque cada vez que escogemos tres letras, hay 3! = 6 formas de revolverlas entre si .Si por cada grupo de 3 letras hay 6 arreglos, entonces el número que buscamos es un sexto del numero de arreglos. Entonces la respuesta que buscamos es 60/6 = 10.
¿Qué habría pasado si en vez de grupos de 3 hubiéramos formado grupos de cuatro?¿o de dos? ¿Y si en vez de un conjunto de 5 elementos hubiésemos comenzado con uno de 10 o de 20?
Para encontrar la formula, supongamos que comenzamos con un conjunto de n elementos y queremos contar de cuantas formas se puede hacer un grupo de k de sus elementos. Al igual que en el razonamiento anterior, comenzamos contando el numero de arreglos de tamaño k. El
teorema 6.4 nos dice que este número es
 Pero al igual que en el ejemplo, este no es el número que buscamos ya que varios arreglos pueden representar el mismo grupo. Pero ya sabemos que k objetos se pueden revolver de k! maneras entre si. Entonces el número de grupos es 1/ k! veces el número de arreglos. De este modo, el número de formas de escoger k elementos a partir de un conjunto con n elementos (sin importar el orden) es
Pero al igual que en el ejemplo, este no es el número que buscamos ya que varios arreglos pueden representar el mismo grupo. Pero ya sabemos que k objetos se pueden revolver de k! maneras entre si. Entonces el número de grupos es 1/ k! veces el número de arreglos. De este modo, el número de formas de escoger k elementos a partir de un conjunto con n elementos (sin importar el orden) es
 Un subconjunto de k elementos de un conjunto con n se llama a veces una combinación, por lo que al número calculado se le llama combinaciones de n en k (o “n en k” por brevedad). También se le da el nombre de coeficiente binomial por razones que aprenderemos más adelante. Se representa de varias maneras algunas de las cuales son entre otras, son:
Un subconjunto de k elementos de un conjunto con n se llama a veces una combinación, por lo que al número calculado se le llama combinaciones de n en k (o “n en k” por brevedad). También se le da el nombre de coeficiente binomial por razones que aprenderemos más adelante. Se representa de varias maneras algunas de las cuales son entre otras, son:
 Resumimos Nuestro trabajo n el siguiente teorema.
Resumimos Nuestro trabajo n el siguiente teorema.
6.5Combinaciones de n en k. El numero de subconjuntos con k elementos de un conjunto con n elementos es
 Las combinaciones juegan un papel central n la combinatoria, por lo que dedicaremos todo el capitulo siguiente al estudio de sus propiedades. Por ahora únicamente nos interesa su aplicación al conteo (cálculos numéricos) .
Las combinaciones juegan un papel central n la combinatoria, por lo que dedicaremos todo el capitulo siguiente al estudio de sus propiedades. Por ahora únicamente nos interesa su aplicación al conteo (cálculos numéricos) .
Ejemplo. El poker se juega con 32 cartas, cada una de las cuales tiene un “número” que puede ser 7,8,9,10,J, Q ,K,A y un símbolo (o “palo”) que puede ser ♠, ♣,♥,♦.De este modo, (10, ♥) representa el diez de corazones. Un jugador recibe 5 cartas.
1.Si de las cinco cartas, hay 3 de u mismo número y dos de otro, ¿de cuántas maneras se puede hacer?
2.Si el jugador recibe cuatro cartas del mismo número (por tanto la última de distinto ¿Cuantos casos posibles hay?
3.¿De cuantas formas puede recibir sus cartas de modo que las cinco sean del mismo palo?
1.Primero usamos el principio de la multiplicación para ver que hay 8 × 7= 56 formas de escoger que número se va a repetir 3 veces y cual se va a repetir dos (porque en total hay 8 números .
Ahora para cada una de esas elecciones, hay que escoger tres cartas de las cuatro que tienen el primer número. Esto puede hacerse de C(4,3) maneras. Para formar las dos restantes , escogemos dos de las cuatro que tienen el segundo número, lo cual puede hacerse de C (4,2) formas. El total de formas es

2.-Hay 8 formas de escoger el número que se repite cuatro veces (que es lo mismo que hacer C (8,1)). La carta restante necesariamente es de un número distinto, porque solo hay cuatro de cada número, así que la podemos escoger de cualquiera de las 28 restantes (en total son 32 cartas) por lo que el número de casos posibles es 8 × 28= 224.
3. El palo tiene cuatro opciones (que es lo mismo que (C 4,1)). De las 8 cartas de cada palo hay que escoger 5. Entonces el total es

 3.-Verifica que
3.-Verifica que 4.-Todos los números de la forma 1007, 10017,100117,1001117,... son divisibles entre 53.
4.-Todos los números de la forma 1007, 10017,100117,1001117,... son divisibles entre 53.



 Entonces tenemos que la suma de los elementos de la diagonal verde y la roja es igual a la suma de los elementos de la diagonal azul. Esto sucede en general si d rdenota la suma de los elementos de la r-ésima diagonal, entonces:
Entonces tenemos que la suma de los elementos de la diagonal verde y la roja es igual a la suma de los elementos de la diagonal azul. Esto sucede en general si d rdenota la suma de los elementos de la r-ésima diagonal, entonces:







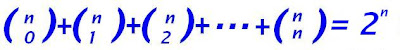








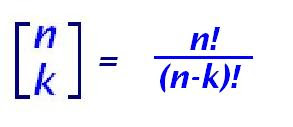
 Así la solución de las palabras de cinco letras la pudimos haber calculado como P (27,22).
Así la solución de las palabras de cinco letras la pudimos haber calculado como P (27,22). 

 Es importante notar que la formula anterior es valida únicamente cuando en todas las posiciones siempre tenemos la misma cantidad de opciones.
Es importante notar que la formula anterior es valida únicamente cuando en todas las posiciones siempre tenemos la misma cantidad de opciones.
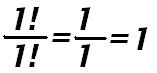









 y así
y así

























