Si en vez de 5 hubiésemos pedido palabras de 10 letras, el numero habría sido 27×26× 25 ×...18, y si en lugar de 10 pidiéramos arreglos de k letras, el total seria
27 × 26 × 25 ×... (27-k +2) × (27-k +1 )
(podemos sustituir varios valores de k para comprobar) ¿Por qué funciona esa formula? En todas las etapas las opciones vienen del mismo conjunto, pero como cada vez que hacemos una elección ya no podemos volver a usa esa letra, las opciones van disminuyendo de una en una, y como hay k posiciones, tenemos k factores consecutivos.
Tampoco tenia nada de especial el 27. La situación general es como sigue: se tiene un conjunto con n objetos (en el ejemplo anterior fue un conjunto de 27 letras), de las cuales se escogen k elementos (en el ejemplo fueron 5) para formar arreglos (palabras), ¿de cuantas formas se puede hacer? La primera posición tiene n opciones, la segunda n-1, la tercera n-2, y así sucesivamente hasta llenar las k posiciones. El total de arreglos es entonces

Teorema 6.4
(Permutaciones de n en k) Si de un conjunto de n elementos se escogen k para formar arreglos, entonces el número de tales arreglos se representa como
Este número también se representa como
Ejemplo. Si en un concurso de matemáticas participan 50 personas, de cuántas maneras pueden quedar repartidos el primer, segundo y tercer lugar?
Para los premiados se escogen 3 de las 50 personas, y como el orden importa, la respuesta es


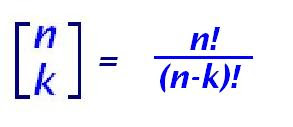

3 comentarios:
creo que n sobre k es n!/(k!·(n-k)!), pero no me hagas mucho caso.....
Julio tú te refieres a comnbinación; el autor habla de permutación
pr favor pueden poner mas ejercicios
Publicar un comentario