Cada uno de estos teoremas se refiere a puntos en los lados de un triángulo, vistos los lados como líneas completas determinadas por pares de vértices del triángulo.
14.2 Teorema de Ceva.
Si tres líneas AO,BO y CO, dibujadas por los vértices de un triángulo ABC y un punto O de su plano, cortan los lados opuestos en L,M y N respectivamente, entonces
 e inversamente , si L, M y N son puntos en los lados BC, CA y AB del triángulo del triángulo ABC para los cuales se cumple la relación anterior, entonces AL, BM y CN son concurrentes.
e inversamente , si L, M y N son puntos en los lados BC, CA y AB del triángulo del triángulo ABC para los cuales se cumple la relación anterior, entonces AL, BM y CN son concurrentes. Hagamos que BM y CN intersequen la paralela a BC que pasa por A , en R y S respectivamente. Entonces por triángulos semejantes tenemos
Hagamos que BM y CN intersequen la paralela a BC que pasa por A , en R y S respectivamente. Entonces por triángulos semejantes tenemos Multiplicando En estas ecuaciones obtenemos
Multiplicando En estas ecuaciones obtenemos  Para probar el inverso, hacemos que BM y CN se intersecten y en O y hagamos que AO corte a BC en L´ entonces tenemos
Para probar el inverso, hacemos que BM y CN se intersecten y en O y hagamos que AO corte a BC en L´ entonces tenemos Pero también
Pero también De lo cual se sigue que
De lo cual se sigue que Entonces L coincide con L´ es decir AL pasa por O, la intersección de BM y CN.
Entonces L coincide con L´ es decir AL pasa por O, la intersección de BM y CN.14.3 Forma trigonométrica del teorema de Ceva.
Teorema : Si la hipótesis del teorema de Ceva se satisface, entonces

 Multiplicando y observando que el producto de la izquierda es igual a la unidad, obtenemos la relación deseada.
Multiplicando y observando que el producto de la izquierda es igual a la unidad, obtenemos la relación deseada.Para el inverso, los pasos en la prueba anterior, pueden ser hechos en el orden inverso, llegando a la relación

14.4 Teorema de Menealo
Teorema. Si una línea recta interseca a los lados BC, CA y AB de un triángulo ABC en los puntos L,M y N respectivamente entonces
Sean AP, BQ y CR las perpendiculares de A, B y C respectivamente a la línea LMN

El inverso puede ser probado haciendo que MN corte a BC en L´ y luego mostrando como se hizo en la sección 3.2 que L coincide con L´.
14.5 Forma trigonométrica del Teorema de Menelao.Teorema : Si la hipótesis del Teorema de Menéalo se satisface, entonces
Las pruebas son tan parecidas a las de la forma trigonométrica de Ceva que no se darán aquí . El lector deberá hacer ambas pruebas .
14. 6 Teorema de división interna y externa.
Ya que AL, BM y CN son concurrentes, tenemos por el teorema de Ceva
Y puesto que L´, M y N son colineales, por el teorema de Menéalo
De lo que obtenemos
De aquí se ve que L y L´ dividen a BC interna y externamente en la misma razón.
En la fig.17 los tres puntos B, L y C están dados; el punto L´ esta determinado de manera única , ya que hay un solo punto que divide el segmento externamente en la misma razón numérica en la que un punto dado divide el segmento internamente. Así podemos concluir lo siguiente:
Sean B, L y C tres puntos fijos en una línea. Si A es un punto cualquiera fuera de esta línea, y M y N son puntos cualesquiera en los lados CA y AB del triángulo ABC de tal forma que AL, BM y CN sean concurrentes, entonces la línea MN intersecará la línea BC en un punto fijo.
Las figuras homotéticas están en perspectiva , pero las figuras en perspectiva, no necesariamente son Homotéticas, puesto que líneas correspondientes de figuras no son paralelas en general.
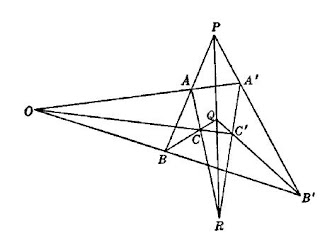
Sean los triángulos ABC y A´B´C´ en perspectiva, con O como centro de perspectiva, y hagamos que AB y A´B´ se corten en P, BC y B´C´ en Q y CA y C´A´ en R. Si aplicamos el teorema de Menéalo al triángulo ABO con B´A´P como transversal, obtenemos

 Y del triángulo CAO con A´C´R como transversal que
Y del triángulo CAO con A´C´R como transversal que
El producto de estas tres ecuaciones nos da
 Que demuestra que P, Q y R son colineales. Ahora, sean dados P, Q y R colineales.
Que demuestra que P, Q y R son colineales. Ahora, sean dados P, Q y R colineales.Ahora sean dados, P, Q y R colineales, y consideremos los triángulos AA´R y BB´Q. Estos triángulos están en perspectiva con P como centro de perspectiva. Más aún O, C y C´ son los puntos de intersección de sus pares de lados correspondientes. Entonces estos tres puntos son colineales; es decir, la línea CC´ pasa por el punto de intersección d AA´ y BB´ .Esto establece el inverso.
La línea en que están P, Q y R es el eje de perspectiva de los triángulos ABC y A´B´C´.
14.9 Importancia el teorema de Desargues. Las propiedades de las figuras geométricas pueden ser clasificadas como métricas y proyectivas. Expresado toscamente, aquellas propiedades que están necesariamente relacionadas, ya sea directa o implícitamente en la noción, a la noción de medida, son propiedades métricas, mientras que aquellas que están esencialmente desconectadas e la medida son propiedades proyectivas. Ejemplos de las primeras son; la igualdad de segmentos de línea ,la semejanza de triángulos, el antiparalelismo de líneas y como ejemplo de las últimas son la concurrencia de líneas y la colinealidad de puntos .La geometría proyectiva es un estudio de las propiedades proyectivas de una configuración .
Lo establecido por el teorema de Desargues , implica sólo propiedades proyectivas de las figuras a las que se aplica. Y como esto está tan relacionado con las ideas de concurrencia y colinealidad, y tales ideas son básicas en la geometría proyectiva , este teorema es uno de los más importantes en este campo. De hecho algunas veces se le toma como el teorema fundamental de la geometría proyectiva.
Es de notarse que, aunque la demostración dada tiene de carácter métrico, es posible dar una demostración que sea completamente de carácter no métrico. Tal demostración es deseable para el desarrollo de la geometría proyectiva, pero desde nuestro punto de vista es interesante ver como se puede demostrar este teorema, tan importante basándose en el Teorema de Menéalo.


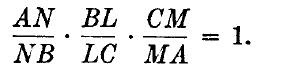


1 comentario:
Excelente!!!
Publicar un comentario